|
郭強(qiáng),陳雪莉,劉海峰
(華東理工大學(xué)煤氣化教育部重點(diǎn)實(shí)驗(yàn)室,上海200237)
摘要:在有限隨機(jī)分裂模型的基礎(chǔ)上,建立針對(duì)生物質(zhì)顆粒破碎的二維有限隨機(jī)分裂模型。模型通過(guò)考察生物質(zhì)顆粒不同方向力學(xué)強(qiáng)度的差異以及子顆粒和母顆粒最小質(zhì)量比等參數(shù),對(duì)生物質(zhì)顆粒的破碎過(guò)程進(jìn)行數(shù)值模擬。通過(guò)對(duì)模擬結(jié)果和實(shí)驗(yàn)結(jié)果的比較,發(fā)現(xiàn)二者具有良好的吻合性,表明二維有限隨機(jī)分裂模型可合理描述生物質(zhì)顆粒的破碎過(guò)程。
0引言
生物質(zhì)的粉碎是生物質(zhì)利用過(guò)程中的一個(gè)重要環(huán)節(jié)。預(yù)測(cè)物質(zhì)破碎后其粒徑分布的模型中,顆粒破碎過(guò)程的描述主要分為瞬時(shí)破碎和連續(xù)破碎兩類,而物料在粉碎機(jī)械中的破碎過(guò)程屬于后者[1]。
1941年,文獻(xiàn)[2,3]提出了固體顆粒破碎的隨機(jī)理論,認(rèn)為顆粒的破碎是離散隨機(jī)過(guò)程,母顆粒破裂成一定數(shù)目的子顆粒的概率與母顆粒的大小無(wú)關(guān)。
1988年,ChengZ等[4]在Kolmogorov理論基礎(chǔ)上提出了線性分裂過(guò)程的自相似性理論。E.Ben-Naim等[5]在保證有穩(wěn)定輸入的基礎(chǔ)上,利用隨機(jī)理論對(duì)破碎過(guò)程進(jìn)行模擬,解決了輸人函數(shù)的時(shí)間依賴性問(wèn)題。
其他研究者[6-8]則在動(dòng)力學(xué)演化方程基礎(chǔ)上對(duì)Kolmogorov的離散隨機(jī)過(guò)程用詳細(xì)的數(shù)學(xué)模型進(jìn)行描述,把Kolmogorov理論中粒徑分布的演化從隨破裂代數(shù)改為隨時(shí)間變化,該理論經(jīng)文獻(xiàn)[9,10]的發(fā)展開(kāi)始應(yīng)用于計(jì)算氣流式霧化過(guò)程的液滴粒徑分布;ZhouWX等[11]用類似方法提出了液滴的隨機(jī)分裂模型,而文獻(xiàn)[12,l3]則在文獻(xiàn)[11]的模型基礎(chǔ)上進(jìn)一步提出有限隨機(jī)分裂模型。然而,上述所研究的顆粒或液滴在宏觀上均表現(xiàn)出各向同性,顆粒或液滴的分裂過(guò)程都屬于一維分裂。考慮到生物質(zhì)顆粒空間結(jié)構(gòu)顯著的各向異性,本文在有限隨機(jī)分裂模型的基礎(chǔ)上,建立描述生物質(zhì)顆粒破碎過(guò)程的二維有限隨機(jī)分裂模型。
1二維有限隨機(jī)分裂模型
1.1模型的基本假定
根據(jù)生物質(zhì)顆粒外形的針狀特性,假定生物質(zhì)顆粒形狀為高度和寬度均為、長(zhǎng)度為Y的長(zhǎng)方體。顆粒整體密度均勻,不隨粒徑的減小而變化。如圖1所示,生物質(zhì)顆粒沿橫向(垂直紋理)和縱向(平行紋理)兩個(gè)方向進(jìn)行破裂,依照Kolmogorov串級(jí)破碎理論,假設(shè)一個(gè)生物質(zhì)顆粒破裂后生成兩個(gè)子顆粒。
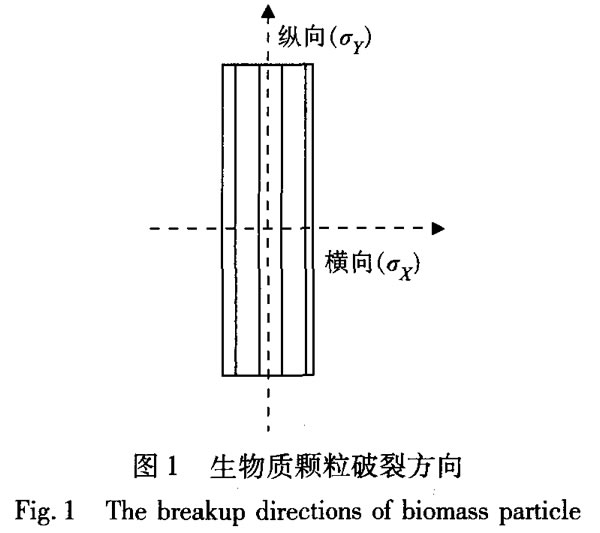
由于生物質(zhì)顆粒破碎時(shí)表現(xiàn)出的各向異性,生物質(zhì)顆粒發(fā)生破碎的方向與生物質(zhì)顆粒的長(zhǎng)寬比以及兩個(gè)方向上的材料強(qiáng)度相關(guān)。生物質(zhì)顆粒破碎過(guò)程中,顆粒破碎后子顆粒和母顆粒的質(zhì)量比m服從[m,1-m]的均勻概率分布,其中0<m<0.5。當(dāng)生物質(zhì)顆粒的平均寬度小于實(shí)驗(yàn)顆粒平均寬度時(shí),破裂停止。
1.2模型中的相關(guān)參數(shù)
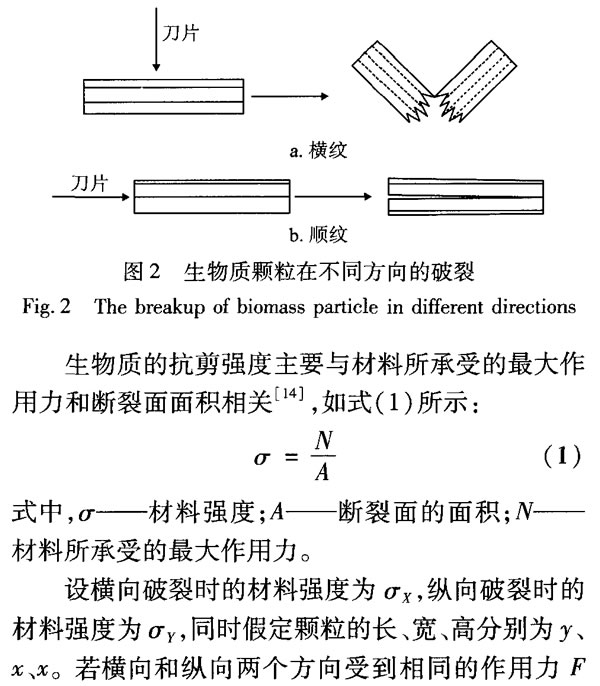
模型中的顆粒進(jìn)行計(jì)算的初始粒徑和實(shí)驗(yàn)中原料進(jìn)入粉碎機(jī)的初始粒徑保持一致。對(duì)于單個(gè)生物質(zhì)顆粒,橫向和縱向的破碎概率分別為Px和Py,橫向和縱向的破碎概率比為K。生物質(zhì)在橫向和縱向方向上機(jī)械性能存在較大差異,這主要是因?yàn)樯镔|(zhì)中作為主要骨架的纖維素在形成過(guò)程中的方向性以及材料內(nèi)部的管狀結(jié)構(gòu)使其在空間結(jié)構(gòu)上存在各向異性。粉碎過(guò)程中,在橫向方向上,如圖2a所示,由于生物質(zhì)材料中纖維素材料的韌性,刀片在接觸顆粒時(shí)會(huì)造成顆粒的變形,顆粒的破裂是內(nèi)側(cè)彎曲而外側(cè)拉伸的過(guò)程,因此橫向方向上抵抗顆粒破碎的是橫紋抗壓強(qiáng)度和順紋抗拉強(qiáng)度的共同作用。
在縱向方向上,如圖2b所示,當(dāng)?shù)镀蜕镔|(zhì)顆粒接觸時(shí),顆粒最先受到的主要是剪切力,因此抵抗顆粒破碎的主要為抗剪強(qiáng)度,而在出現(xiàn)裂紋后,隨著刀片的切入,變?yōu)榭v向方向的劈裂過(guò)程。然而在此模型中,由于粉碎機(jī)刀片具有相對(duì)較高的轉(zhuǎn)速(24000r/min),刀片與生物質(zhì)顆粒的接觸時(shí)間較短,故認(rèn)為生物質(zhì)顆粒破碎過(guò)程中材料強(qiáng)度不發(fā)生變化。

1.3模型計(jì)算過(guò)程
模擬初始,以原料進(jìn)入粉碎機(jī)的粒徑作為第一代破碎顆粒,按照顆粒在兩個(gè)方向上不同的破碎概率確定發(fā)生顆粒發(fā)生破裂的方向,進(jìn)行隨機(jī)位置的破裂,得到的子顆粒為第二代顆粒。將第二代顆粒寬度的平均值與實(shí)驗(yàn)值進(jìn)行比較。若符合收斂條件則停止計(jì)算,否則第二代顆粒繼續(xù)進(jìn)行破裂,以此類推,直至結(jié)果收斂,此時(shí)所獲得的顆粒即作為粉碎得到的最終顆粒。將此時(shí)的顆粒依照寬度進(jìn)行分級(jí),求取不同范圍內(nèi)顆粒所占的體積分率,由于假定顆粒密度不變,所以體積分率和質(zhì)量分率相等,從而獲得粒徑分布。調(diào)整c和m值,利用最小二乘法比較實(shí)驗(yàn)與模擬結(jié)果,從而獲得最優(yōu)結(jié)果。
2模擬結(jié)果分析
2.1實(shí)驗(yàn)
實(shí)驗(yàn)中所使用的原料為松木、豆秸、稻稈和蘆葦4種生物質(zhì),其中松木來(lái)源于上海某家具廠,豆秸、稻稈和蘆葦均來(lái)自上海市南匯區(qū)。實(shí)驗(yàn)所用的粉碎機(jī)為天津泰斯儀器有限公司生產(chǎn)的Fw177型微型植物粉碎機(jī),轉(zhuǎn)速24000r/min,粉碎效果為60~200目。松木、豆秸、稻稈和蘆葦4種生物質(zhì)原料進(jìn)人粉碎機(jī)的平均初始粒徑分別為60mm×10mm,100mm×7mm,100mm×6mm和100mm×10mm。生物質(zhì)粉碎前均為自然風(fēng)干,其含水量見(jiàn)表1。

生物質(zhì)原料經(jīng)粉碎機(jī)3min粉碎后,篩分為0.300~0.425mm、0.180~0.300mm、0.150—0.180mm、0.106~0.150mm及0.083~0.106mm5個(gè)不同的粒徑范圍。最后,通過(guò)計(jì)算不同粒徑范圍內(nèi)的質(zhì)量分率,獲得顆粒的粒徑分布(表2)。
顆粒長(zhǎng)和寬的測(cè)量方法主要按照如下定義:顆粒的寬度定義為顆粒投影圖像的相距最近兩平行線間的距離,垂直其方向定義為長(zhǎng)度方向。粉碎停止后,利用顯微鏡對(duì)隨機(jī)抽取的300個(gè)生物質(zhì)顆粒進(jìn)行拍照,測(cè)量其獲得的顆粒圖像,按照相應(yīng)的放大比例獲得顆粒寬度的真實(shí)值,計(jì)算其粉碎后的平均寬度。
2.2模擬
基于前文的假設(shè),對(duì)生物質(zhì)顆粒的破碎過(guò)程進(jìn)行模擬計(jì)算。設(shè)定初始生物質(zhì)顆粒的數(shù)量為105個(gè),以顆粒的寬度作為篩分粒徑,當(dāng)顆粒平均寬度小于實(shí)驗(yàn)值時(shí),計(jì)算停止,然后計(jì)算不同粒徑范圍內(nèi)的顆粒數(shù)量以及單個(gè)顆粒的體積,求出顆粒總體積及體積分率。由于假設(shè)顆粒密度不隨粒徑發(fā)生變化,故對(duì)于同一種生物質(zhì)而言,體積分率和質(zhì)量分率相等。經(jīng)過(guò)計(jì)算,式(6)中的顆粒材料強(qiáng)度之比c值如表3所示,而顆粒破碎過(guò)程中,子顆粒和母顆粒的最小質(zhì)量比m值見(jiàn)表4。
由表3可知,盡管生物質(zhì)顆粒存在各向異性,但對(duì)同一種生物質(zhì)而言,在其破碎過(guò)程中,兩個(gè)方向破碎后產(chǎn)生的子顆粒和母顆粒的最小質(zhì)量比m一致,說(shuō)明顆粒發(fā)生破裂的位置受顆粒兩個(gè)方向上的絕對(duì)長(zhǎng)度的影響并不明顯。然而對(duì)于不同的生物質(zhì),C值越小,材料各向異性越強(qiáng),m值越小,分裂后產(chǎn)生的顆粒大小差距越大。這是因?yàn)樯镔|(zhì)材料各向異性越強(qiáng),生物質(zhì)顆粒的針狀特性越明顯,顆粒發(fā)生破碎的范圍越大。圖3為0.180~0.300mm粒徑范圍內(nèi),借助顯微鏡所測(cè)得的4種生物質(zhì)顆粒的平均長(zhǎng)寬比am與m的關(guān)系,線性擬合后如式(7)所示,相關(guān)系數(shù)R>0.99。
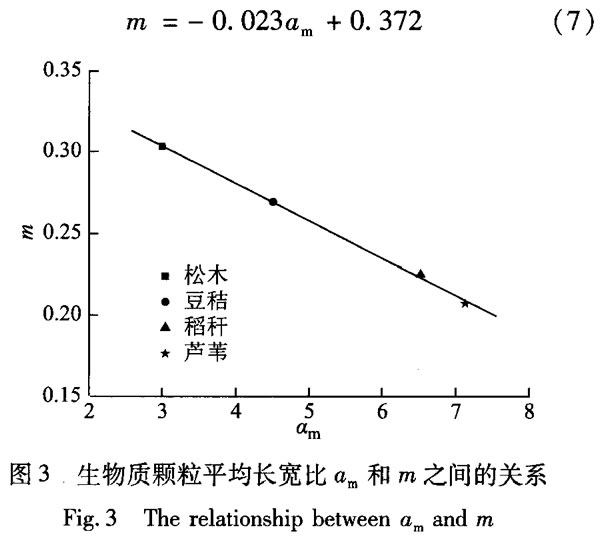
從圖3可看出,生物質(zhì)材料各向異性越強(qiáng),不同方向強(qiáng)度差異越大,破碎后所得到的顆粒外形更加細(xì)長(zhǎng)。因此對(duì)于粒徑(顆粒寬度)相等的生物質(zhì)顆粒,各向異性越強(qiáng),其顆粒長(zhǎng)度也越長(zhǎng)。若顆粒和刀片發(fā)生接觸后所分裂出的最小的子顆粒的大小一定,那么更加細(xì)長(zhǎng)的顆粒發(fā)生隨機(jī)破裂的位置范圍就越廣,即m值越小,所以m值隨著c值的減小而減小是合理的。
2.3模擬結(jié)果和實(shí)驗(yàn)結(jié)果比較
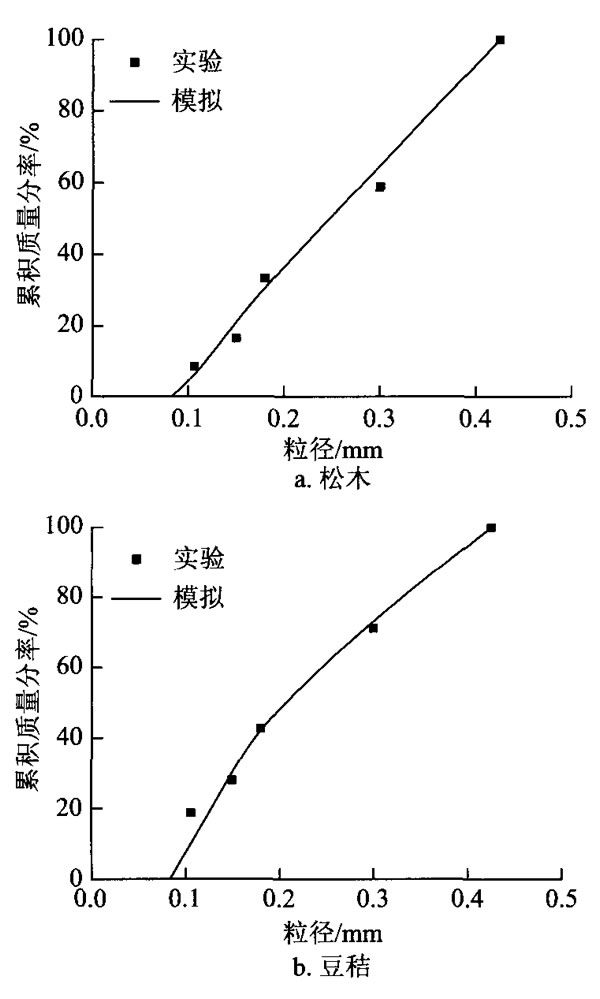
從圖4可看出,4種生物質(zhì)粒徑分布的模擬結(jié)果和實(shí)驗(yàn)結(jié)果較為吻合。根據(jù)文獻(xiàn)[15]所述,木材遭受破壞時(shí)存在的5種強(qiáng)度分別為:抗劈強(qiáng)度、順紋抗剪強(qiáng)度、橫紋抗拉強(qiáng)度、橫紋抗壓強(qiáng)度以及順紋抗拉強(qiáng)度,其強(qiáng)弱關(guān)系為:抗劈強(qiáng)度<橫紋抗拉強(qiáng)度<順紋抗剪強(qiáng)度<橫紋抗壓強(qiáng)度<順紋抗拉強(qiáng)度。在松木顆粒的破碎過(guò)程中,縱向方向破裂近似劈裂過(guò)程,而橫向方向則是近似處于橫紋壓縮和順紋拉伸兩者之間。由文獻(xiàn)[16]中所提出關(guān)于松木強(qiáng)度的實(shí)驗(yàn)值可知,松木的抗劈強(qiáng)度為4.998×10-3N/m2,橫紋抗壓強(qiáng)度為0.3224N/m2,順紋抗拉強(qiáng)度為1.0780N/m2,所以松木顆粒在破碎過(guò)程中,兩個(gè)方向上的材料強(qiáng)度之比應(yīng)在0.0046—0.0150之間,而在模擬結(jié)果中,松木縱向和橫向的材料強(qiáng)度之比為0.012(見(jiàn)表3),恰好在這個(gè)范圍之內(nèi),因此二維有限隨機(jī)分裂模型可對(duì)松木顆粒的破碎過(guò)程進(jìn)行模擬。而對(duì)于其他3種生物質(zhì),盡管難以測(cè)試其材料強(qiáng)度,進(jìn)而驗(yàn)證c值的準(zhǔn)確性,但由于其他3種生物質(zhì)均為一年生草本植物,在其生長(zhǎng)過(guò)程中,細(xì)胞的分裂主要是沿其生長(zhǎng)方向(即縱向方向),橫向方向分裂有限,這使其纖維結(jié)構(gòu)的各向異性更加明顯,所以c值和松木相比偏小也較為合理。

3結(jié)論
1)結(jié)合生物質(zhì)材料空間結(jié)構(gòu)各向異性所導(dǎo)致的材料強(qiáng)度在不同方向上的差異,在有限隨機(jī)分裂模型的基礎(chǔ)上,建立了描述各向異性生物質(zhì)顆粒破碎過(guò)程的二維有限隨機(jī)分裂模型,對(duì)生物質(zhì)顆粒的破碎過(guò)程進(jìn)行數(shù)值模擬。
2)松木、豆秸、稻稈和蘆葦4種生物質(zhì)顆粒粒徑分布的模擬結(jié)果和實(shí)驗(yàn)結(jié)果具有良好的吻合性,表明通過(guò)對(duì)模型中參數(shù)的確定,二維有限隨機(jī)分裂模型可對(duì)生物質(zhì)粉碎后的粒徑分布進(jìn)行合理的預(yù)測(cè)。
3)模型中各項(xiàng)參數(shù)物理意義明確,其中C值的結(jié)果表明二維有限隨機(jī)分裂模型可對(duì)生物質(zhì)材料的各向異性進(jìn)行合理描述。顆粒在破碎時(shí),兩個(gè)方向上的m值的一致性說(shuō)明對(duì)于同一種生物質(zhì)顆粒,發(fā)生破裂的位置受顆粒長(zhǎng)度和寬度絕對(duì)值的影響并不明顯;但對(duì)于不同的生物質(zhì),材料的各向異性越強(qiáng),針狀特性越明顯,顆粒發(fā)生隨機(jī)破裂的位置范圍越大,分裂產(chǎn)生的子顆粒的大小差距也越大。
[參考文獻(xiàn)]
[1]Ast?m J A.Statistical models of bittle fragmentation[J].Advances in Physics,2006,55(3-4):247-278.
[2]Kolmogorov A N.On the 10g-norml distibution of particles sizes duing breakup process[J].Dokl Akad Nnk,1941,SSSR XXXI(2):99-101.
[3]Lefebvre A H.Atomization and sprays[M].New York:Hemisphere Publishing Corporation,1989.
[4]Cheng Z,Redner S.Scling theory of fagmentMion[J].Physicl Review Letters,1988,60(24):2450-2453.
[5]Ben-Naim E,Krapivsky P L.Fragmentation with a steady source[J].Physics Letters A,2000,275(1-2):48-53.
[6]Ernst M H,Szmmel G.Fragmentation kinetics[J].Jounal of Physics A:Mathematical and Generl.1993,26(22):6085-6091.
[7]Treat R P.On the similaity solution of the fragmentation equation[J].Jounal of Physics A:Mathematical and General,1997,3o(7):2519-2543.
[8]Huang J,Guo X,Edwards B F,et al.Cut-of model and exact general solutions for fragmentation with mass loss[J].Jounal of Physics A:Mathematicl and
General,1996,29(23):7377-7388.
[9]Gorokhovski M A,Saveliev V L.Anlyses of Kolmogorov’S model of breakup and its application into Lagrangian computation of liquid sprays under air-blast
atomization[J].Physics of Fluids,2003,15(1):184-192.
[10]Apte S V,Gorokhovski M,Moin P.LES of atomizing spray with stochastic modeling of seconday breakup[J].Intenational Journal of Multiphase Flow,2003,29(9):1503-1522.
[11]Zhou W X,Zhao T J,Wu T,et al.Application of fractal geomety to atomization process[J].Chemical Engineeing Jounl,2000,78(2-3):193-197.
[12]龔 欣,劉海峰,李偉鋒,等.氣流式霧化過(guò)程的有限隨機(jī)分裂模型[J].化工學(xué)報(bào),2005,56(5):786-790.
[12]Gong Xin,Liu Haifeng,Li Weifeng,et al.Finite stochastic breakup model of air-blast atomization process[J].Jouml of Chemical Industy and Engineeing(China),2005,56(5):786-790.
[13]Liu H F,Gong X,Li W F,et al.Prediction of droplet size distibution in sprays of preilming air-blast atomizers[J].Chemicl Engineeing Science,2006,61(6):1741-1747.
[14]Womac A R,Yu M,Igathinathane C,et al.Shearing characteistics of biomass for size seduction[A].ASABE[C],St Joseph,2005.
[15]Heywood H.Numeicl deinitions of particle size and shape[J].Chemistry nd Industy,1937,56(7):149-l54.
[16]Kollmann F F P,Cote W A.木材學(xué)與木材工藝學(xué)原理一實(shí)體木材[M].北京:中國(guó)林業(yè)出版社,1991. |
